Ulrich von Augsburg (Reiter mit Pferd)

Dieses Origami Modell habe ich im Mai 2024 entworfen. Es ist mein erstes Design, das überwiegend auf dem Papier entstanden ist, ohne dass ich währenddessen zum Testen gefaltet habe, und auch mein erster Versuch, ein etwas komplexeres Subjekt umzusetzen. Ulrich von Augsburg war von 923 bis 973 Bischof von Augsburg. Die Darstellung zeigt das berühmte Bild der Schlacht auf dem Lechfeld im Jahr 955, in der Ulrich ein Kreuz erhält. Reiter und Pferd sind aus einem Papier.

Zum Falten habe ich ein etwas größeres Kalligraphiepapier (37 x 37 cm) verwendet, das dünn und reißfest ist, und somit ausgezeichnet für ein anspruchsvolleres Origami Modell wie dieses. Die Basis lässt sich in etwa einer Stunde falten, um allerdings zum fertigen Modell zu gelangen, sind noch einige weitere Stunden Arbeit nötig. Da ich selbst bis auf das Circle packing keine Vorlage hatte, musste ich auch ein bisschen probieren, um die Form des Pferdes und die Menschenfigur einigermaßen hinzubekommen.
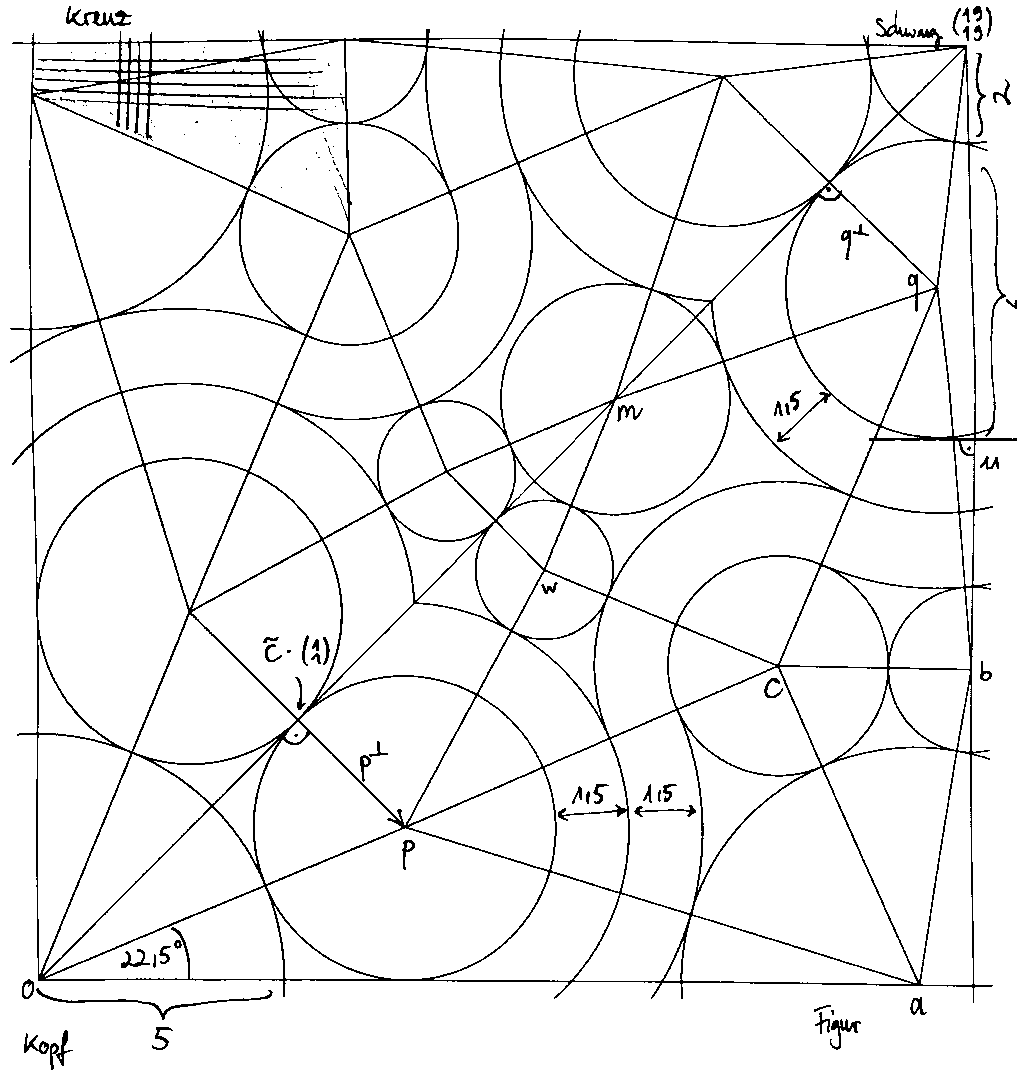
Pferd, Figur und Kreuz sind aus einem ungeschnittenen, quadratischen Papier. Welche Teile des Papiers zu welchen ELementen geformt werden, ist in der Skizze beschrieben.

Das Design basiert grob auf einem 19 x 19 Gitter, wobei die Längenangaben in der annotierten Skizze in diesem Kontext zu interpretieren sind. Die Koordinaten der Punkte \( p,q,a,b,c,w,m \) kann man durch Lösen von Gleichungssystemen ausrechnen. Das Modell verwendet die eingezeichnete Diagonale als Hauptachse und die Basis ist achsensymmetrisch. Die unregelmäßigen Vierecke sind mit den von Robert Lang beschriebenen gusset molecules aufzufüllen, bei den Dreiecken und dem Trapez ergänzt man die Falten entlang der Winkelhalbierenden in jeder Ecke. Zur Bestimmung der Koordinaten der Punkte kann man wie folgt vorgehen, hier ein Beispiel für den Punkt \( p \):

Es gilt zunächst, dass \( p \) auf der 22,5°-Geraden durch den Ursprung liegt, d. h. \( p_2 = \tan\left(\frac{\pi}{8}\right)\cdot p_1 = \bigl(\sqrt{2}-1\bigr) p_1 \) (mehr dazu weiter unten unter Berechnung von \( \tan{\frac{\pi}{8}} \)). Desweiteren hat der Kreis um \( p \) einen Radius von \( r = \|p\| - 5 \). Gleichseitig soll der Kreis die Diagonalachse berühren, also ist außerdem \( r = \| p^\perp \| \), wobei \( p^\perp \perp \left(\begin{smallmatrix}1\\1\end{smallmatrix}\right) \). Zusammen mit \( p^\perp = p - \widetilde c \left(\begin{smallmatrix}1\\ 1\end{smallmatrix}\right) \) kann man daraus kann man die Orthogonalprojektion von \( p \) auf \( \left(\begin{smallmatrix}1\\ 1\end{smallmatrix}\right) \) berechnen: \[ 0 = \left\langle \begin{pmatrix}1\\1\end{pmatrix},\,p^\perp \right\rangle =\left\langle \begin{pmatrix}1\\1\end{pmatrix},\,p-\widetilde{c}\begin{pmatrix}1\\1\end{pmatrix} \right\rangle =p_1+p_2-2\widetilde{c} \] Damit ist \( \widetilde c=\frac{p_1+p_2}{2},\quad \) \( p^\perp = p - \left(\begin{smallmatrix}(p_1+p_2)/2)\\ (p_1+p_2)/2\end{smallmatrix}\right) \) \( =\left(\begin{smallmatrix}(p_1-p_2)/2)\\ (p_2-p_1)/2\end{smallmatrix}\right) \) und \( \| p^\perp \| = \frac{|p_1-p_2|}{\sqrt{2}} \). Die Rechnung soll hier beispielhaft für die Seite unter der Diagonalen sein, daher kann man \( p_1 \ge p_2 \) voraussetzen und den Betrag weglassen (und es gilt grundsätzlich \( p\ge0 \)). Durch Gleichsetzen von \( \|p^\perp\| = \|p\| - 5 \) erhält man dann ein Gleichungssystem: \begin{align*} \frac{p_1 - p_2}{\sqrt{2}} &= \sqrt{p_1^2 + p_2^2} - 5 \tag{1}\\ p_2 &= \bigl(\sqrt{2}-1\bigr) p_1 \tag{2} \end{align*} Durch Einsetzen von 2 in 1 erhält man: \begin{align*} &\bigl(\sqrt{2}-1\bigr)p_1 = \sqrt{4-2\sqrt{2}} \cdot p_1 - 5\\ \iff{} &p_1 = 5\left(\sqrt{4-2\sqrt{2}} + \sqrt{2} - 1\right) \approx 7.483028813\\ &p_2 = \bigl(\sqrt{2}-1\bigr)p_1 = 5\left(\sqrt{20-14\sqrt{2}} + 3 - 2\sqrt{2}\right) \approx 3.099572022 \end{align*} Der Radius des Kreises ist genau der Abstand zur \( x_1 \)-Achse, also ist auch \( r = 3.099572022 \).

Die Berechnung von \( q \) verläuft analog. Wieder ist \( \widetilde r = \|q^\perp\| = \frac{q_1-q_2}{\sqrt{2}} \) und \( \widetilde r = \left\| \left(\begin{smallmatrix}19\\ 19\end{smallmatrix}\right) - q \right\| - 2 \). Um eine eindeutige Lösung zu erhalten sei noch festgelegt, dass der Kreis um \( q \) unten genau die Höhe 11 berühren soll. Es ergibt sich wieder ein Gleichungssystem: \begin{align*} q_2 &= 11 + \widetilde r \tag{1}\\ \widetilde r &= \left\| \begin{pmatrix}19\\ 19\end{pmatrix} - q \right\| - 2 \tag{2}\\ \widetilde r &= \frac{q_1-q_2}{\sqrt{2}} \tag{3} \end{align*} Durch Gleichsetzen von 1 und 3 erhält man: \begin{align*} &q_2 - 11 = \frac{q_1-q_2}{\sqrt{2}}\\ \iff{} &q_1 = \bigl(\sqrt{2} + 1\bigr)q_2 - 11\sqrt{2} \tag{4} \end{align*} Dann kann man 1 und 2 gleichsetzen und 4 in die Gleichung einsetzen. Nach Quadrieren und weiteren Umformungen erhält man folgende Gleichung, die man mit der Lösungsformel für quadratische Gleichungen lösen kann: \[ \bigl(3+2\sqrt{2}\bigr) q_2^2 - \bigl(102+60\sqrt{2}\bigr) q_2 + \bigl(883+418\sqrt{2}\bigr) = 0 \] Es gibt nur eine sinnvolle Lösung, die andere liegt außerhalb des 19 x 19 Gitters:
\( q_1\approx 18.301531 \) und \( q_2\approx 14.024393 \)

Für die übrigen Punkte \( a,b,c,w,m \) kann man ähnlich vorgehen. Wichtig zu beachten ist nur, dass die Kreise immer maximal ausgedehnt werden. Deutlich schneller und einfacher ist es, die Punkte mit einem Computerprogramm berechnen zu lassen.

Additionstheoreme: \begin{align*} &\cos(\alpha+\beta) + i \sin(\alpha+\beta) = e^{i(\alpha+\beta)}\\ &= e^{i\alpha}\cdot e^{i\beta} = (\cos{\alpha} + i\sin{\alpha})(\cos{\beta} + i\sin{\beta})\\ &= \cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta} + i(\sin{\alpha}\cos{\beta} + \sin{\beta}\cos{\alpha}) \end{align*} \begin{align*} \implies &\cos(\alpha+\beta) =\cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta}\\ &\cos(2\alpha)=\cos^2{\alpha} - \sin^2{\alpha} \tag{1}\\ \implies &\sin(\alpha+\beta) =\sin{\alpha}\cos{\beta} + \sin{\beta}\cos{\alpha}\\ &\sin(2\alpha)=2\sin{\alpha}\cos{\alpha} \tag{2} \end{align*} Zunächst berechnet man \( \sin{\frac{\pi}{4}} \): \[ 1 = \sin{\frac{\pi}{2}} = 2\sin{\frac{\pi}{4}}\cos{\frac{\pi}{4}} =2\sin{\frac{\pi}{4}}\sin\left(\frac{\pi}{2} - \frac{\pi}{4}\right) = 2\sin^2\left(\frac{\pi}{4}\right) \] \[ \implies \sin{\frac{\pi}{4}} = \frac{\sqrt{2}}{2},\quad \cos{\frac{\pi}{4}} = \frac{\sqrt{2}}{2} \] Mit (1): \[ \cos{\alpha} = \cos^2{\frac{\alpha}{2}} - \sin^2{\frac{\alpha}{2}} =\cos^2{\frac{\alpha}{2}} - \left(1-\cos^2{\frac{\alpha}{2}}\right) = 2\cos^2{\frac{\alpha}{2}} - 1 \] \[ \cos{\frac{\alpha}{2}} = \sqrt{\frac{1+\cos{\alpha}}{2}},\quad \cos{\frac{\pi}{8}} =\sqrt{\frac{1+\cos{\frac{\pi}{4}}}{2}} = \sqrt{\frac{1+\sqrt{2}/2}{2}} \] \[ \cos{\alpha} = \cos^2{\frac{\alpha}{2}} - \sin^2{\frac{\alpha}{2}} =\left(1-\sin^2{\frac{\alpha}{2}}\right) - \sin^2{\frac{\alpha}{2}} = 1-2\sin^2{\frac{\alpha}{2}} \] \[ \sin{\frac{\alpha}{2}} = \sqrt{\frac{1-\cos{\alpha}}{2}},\quad \sin{\frac{\pi}{8}} =\sqrt{\frac{1-\cos{\frac{\pi}{4}}}{2}} = \sqrt{\frac{1-\sqrt{2}/2}{2}} \] \[ \tan{\frac{\pi}{8}} = \frac{\sin{\frac{\pi}{8}}}{\cos{\frac{\pi}{8}}} = \sqrt{\frac{1-\sqrt{2}/2}{1+\sqrt{2}/2}} = \sqrt{2\cdot\bigl(1-\sqrt{2}/2\bigr)^2} = \sqrt{2}\left(1-\frac{\sqrt{2}}{2}\right) = \sqrt{2} - 1 \]