Dodekaeder, Fünfecke und Trigonometrie

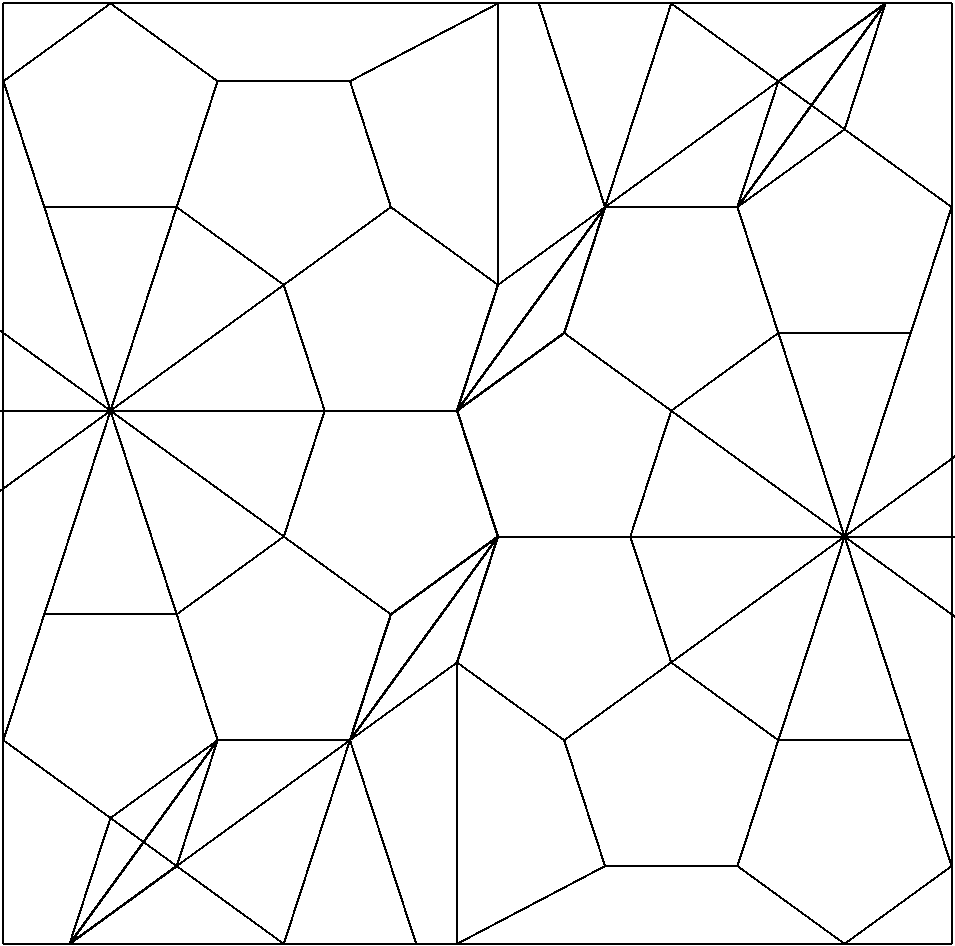
Hier kann das Crease Pattern des Dodekaeder zum Nachfalten heruntergeladen werden und auf gewöhnlichem Druckerpapier (empfohlene Größe: A4) ausgedruckt und ausgeschnitten werden. Die Vorlage ist nicht perfekt quadratisch, eine Seite ist etwa 1 mm länger. Es ist aber auch möglich das Dodekaeder aus einem quadratischen Papier zu falten, da der Überschuss im Modell versteckt und somit unsichtbar ist und die Abweichung klein genug ist, dass keine Unschönheiten aufgrund der Genauigkeit entstehen. Im Folgenden finden Interessierte eine Beschreibung, wie das Dodekaeder aus einem quadratischen Blatt Papier ohne weitere Hilfsmittel gefaltet werden kann. Die Faltanleitung für das Origami Dodekaeder und der Konstruktion des zugrundeliegenden Fünfecks findet sich weiter unten, einfacher ist es aber, das Crease Pattern auszudrucken.

Das Dodekaeder ist der platonische Körper, der am schwierigsten aus einem quadratischen Papier zu konstruieren ist. Während die anderen platonischen Körper als Seitenflächen gleichseitige Dreiecke oder Quadrate haben, wobei beide ziemlich einfach zu konstruieren sind (für gleichseitige Dreiecke wurde z. B. eine Methode von Fujimoto beschrieben), sind die Seitenflächen des Dodekaeders regelmäßige Fünfecke. Die Innenwinkel eines regelmäßigen Fünfecks sind \( \frac{(5-2)\pi}{5} = \frac{3\pi}{5} \), bzw. 108°. Dazu ein kleiner Exkurs, da viele Sätze aus der euklidischen Geometrie in der Schule unbegründet bleiben und die Beweise später meist zu einfach sind, um nochmal aufgegriffen zu werden:

Neben der Herausforderung der Konstruktion der \( \frac{\pi}{5} \)-Winkel müssen die Fünfecke noch effizient auf dem quadratischen Ausgangsformat verteilt werden und außerdem sollte das Modell am Ende stabil sein. Im Folgenden möchte ich eine kurze Anleitung und Herleitung geben, wie man den 72° und 108° Winkel für dieses Dodekaedermodell konstruiert:

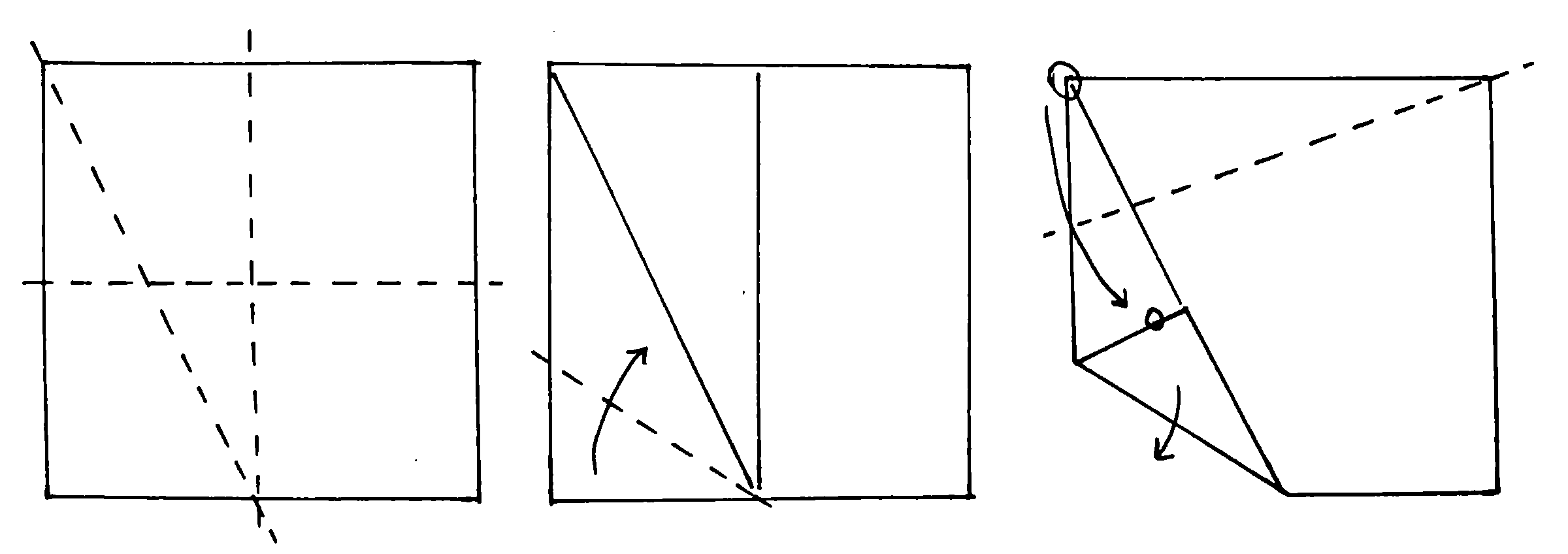
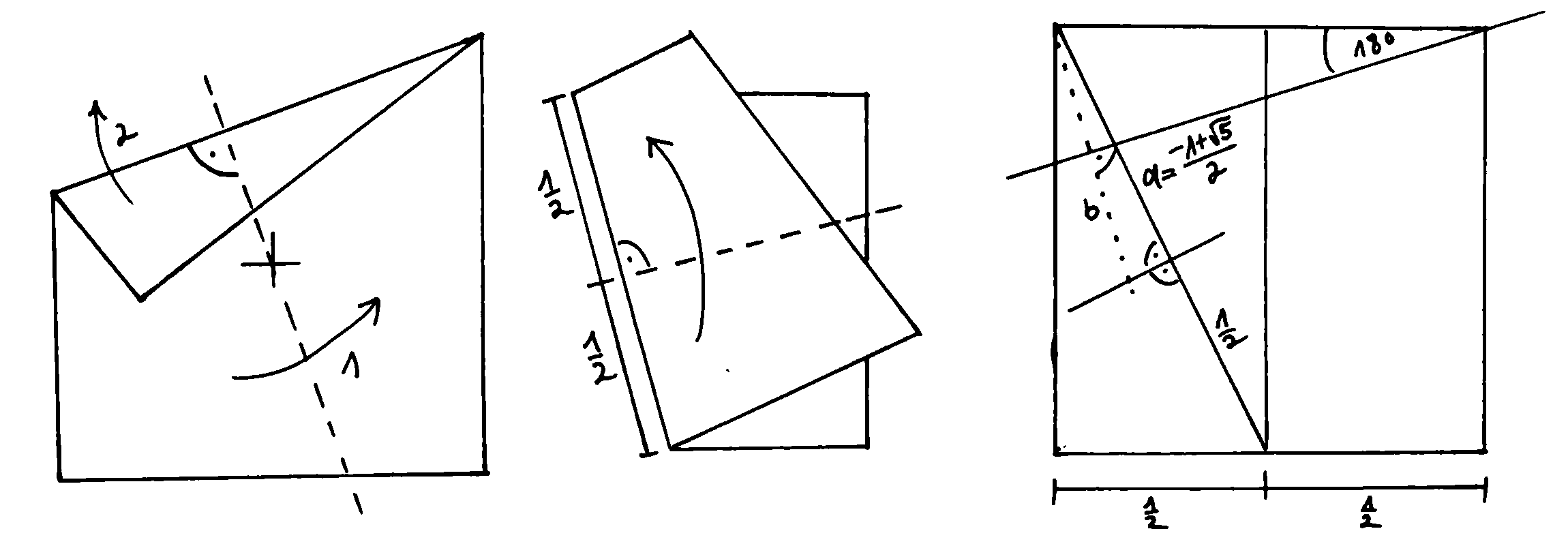
Die Länge von \( a \) ergibt sich aus \( a=\sqrt{1^2 + \left(\frac{1}{2}\right)^2} - \frac{1}{2} \). Mit der Kleinwinkelnäherung (hier \( \cos{x}\approx 1 \)) kann man die Länge \(b\) mit \( a \) approximieren \( (\pm 1\%) \), wobei \(b\) orthogonal zu der Winkelhalbierenden des 36° Winkels ist. Damit lässt sich der Winkel \( \alpha \), der hier mit 18° gekennzeichnet ist, berechnen mit \( \alpha=\arcsin{\frac{\frac{-1+\sqrt{5}}{4}}{1}} \). Hier ist eine elementare Möglichkeit, \( \sin{\frac{\pi}{10}} \) auszurechnen, um zu zeigen, dass es sich tatsächlich um einen 18° Winkel handelt. Dazu betrachtet man zunächst \( \frac{\pi}{5} \):
\begin{align*} \cos(5\alpha) + i\sin(5\alpha) &= e^{5i\alpha} = \left(e^{i\alpha}\right)^5\\ = (\cos\alpha+i\sin\alpha)^5 &=\sum_{k=0}^5 \binom{5}{k}\cos^{(5-k)}(\alpha)\cdot i^k\sin^k(\alpha) \end{align*} Durch Koeffizientenvergleich stellt man fest, dass zur Berechnung von \( \sin(5\alpha) \) nur die ungeraden Summanden relevant sind: \begin{align*} \sin(5\alpha) &= \binom{5}{1}\cos^{(5 - 1)}(\alpha)\sin(\alpha) -\binom{5}{3}\cos^{(5-3)}(\alpha)\sin^3(\alpha) + \binom{5}{5}\cos^{(5-5)}(\alpha)\sin^5(\alpha)\\ &=5\cos^4(\alpha)\sin(\alpha) - 10\cos^2(\alpha)\sin^3(\alpha) + \sin^5(\alpha)\\ &=5\bigl(1-\sin^2(\alpha)\bigr)^2\sin(\alpha) - 10\bigl(1-\sin^2(\alpha)\bigr)\sin^3(\alpha) + \sin^5(\alpha)\\ &=5\sin(\alpha) - 20\sin^3(\alpha) + 16\sin^5(\alpha) \end{align*} Für \( \alpha=\frac{\pi}{5} \) erhält man \[ 0=\sin{\pi}=5\sin\left(\frac{\pi}{5}\right) - 20\sin^3\left(\frac{\pi}{5}\right) + 16\sin^5\left(\frac{\pi}{5}\right) \] und schließlich durch Ausklammern von \( \sin\frac{\pi}{5} \) und Substitution mit \( x = \sin^2\left(\frac{\pi}{5}\right) \ne 0 \): \[ 5 - 20x + 16x^2 = 0 \iff x = \frac{5\pm \sqrt{5}}{8}. \] Also ist \( \sin\frac{\pi}{5}\in\left\{\pm\sqrt{\frac{5\pm \sqrt{5}}{8}}\right\} = \left\{\pm\frac{\sqrt{10\pm 2\sqrt{5}}}{4}\right\} \). Wegen \( \sin\frac{\pi}{5} > 0 \) und \( \frac{\mathrm{d}}{\mathrm{d}x}\sin{x} \le 1 \) \( (\text{d. h.}\,\sin\frac{\pi}{5} \le \frac{\pi}{5}) \) bleibt nur noch \[ \sin{\frac{\pi}{5}} = \frac{\sqrt{10 - 2\sqrt{5}}}{4}. \] und \begin{align*} \cos{\frac{\pi}{5}} &= \sqrt{1 - \frac{10 - 2\sqrt{5}}{16}} = \frac{\sqrt{6 + 2\sqrt{5}}}{4}\\ &= \frac{\sqrt{5 + 2\sqrt{5} + 1}}{4} = \frac{1+\sqrt{5}}{4} \end{align*} Um nun auf \( \sin{\frac{\pi}{10}} \) zu schließen, folgert man aus den Additionstheoremen \( \cos(2\theta) = \cos(\theta+\theta) = \cos^2(\theta)-\sin^2(\theta) \) und erhält \begin{align*} &\cos\left(2\cdot\frac{\pi}{10}\right) = 1-2\sin^2\left(\frac{\pi}{10}\right)\\ &\Leftrightarrow \sin^2\left(\frac{\pi}{10}\right) = \frac{1 - \frac{1+\sqrt{5}}{4}}{2}\\ &\Leftrightarrow \sin\frac{\pi}{10} = \sqrt{\frac{3-\sqrt{5}}{8}} = \frac{\sqrt{6 - 2\sqrt{5}}}{4} = \frac{-1+\sqrt{5}}{4}, \end{align*} wobei im letzten Schritt zum Ausrechnen mit \( \frac{\sqrt{2}}{\sqrt{2}} \) erweitert wurde.

Damit ist also gezeigt, dass \( \sin{\frac{\pi}{10}} \) tatsächlich dieselbe Länge wie in der obigen Konstruktionsskizze ist und der Winkel in der rechten oberen Ecke etwa 18° hat.

Ausgehend vom Resultat der Faltsequenz oben kann man nun mit der Referenzfindung weitermachen.

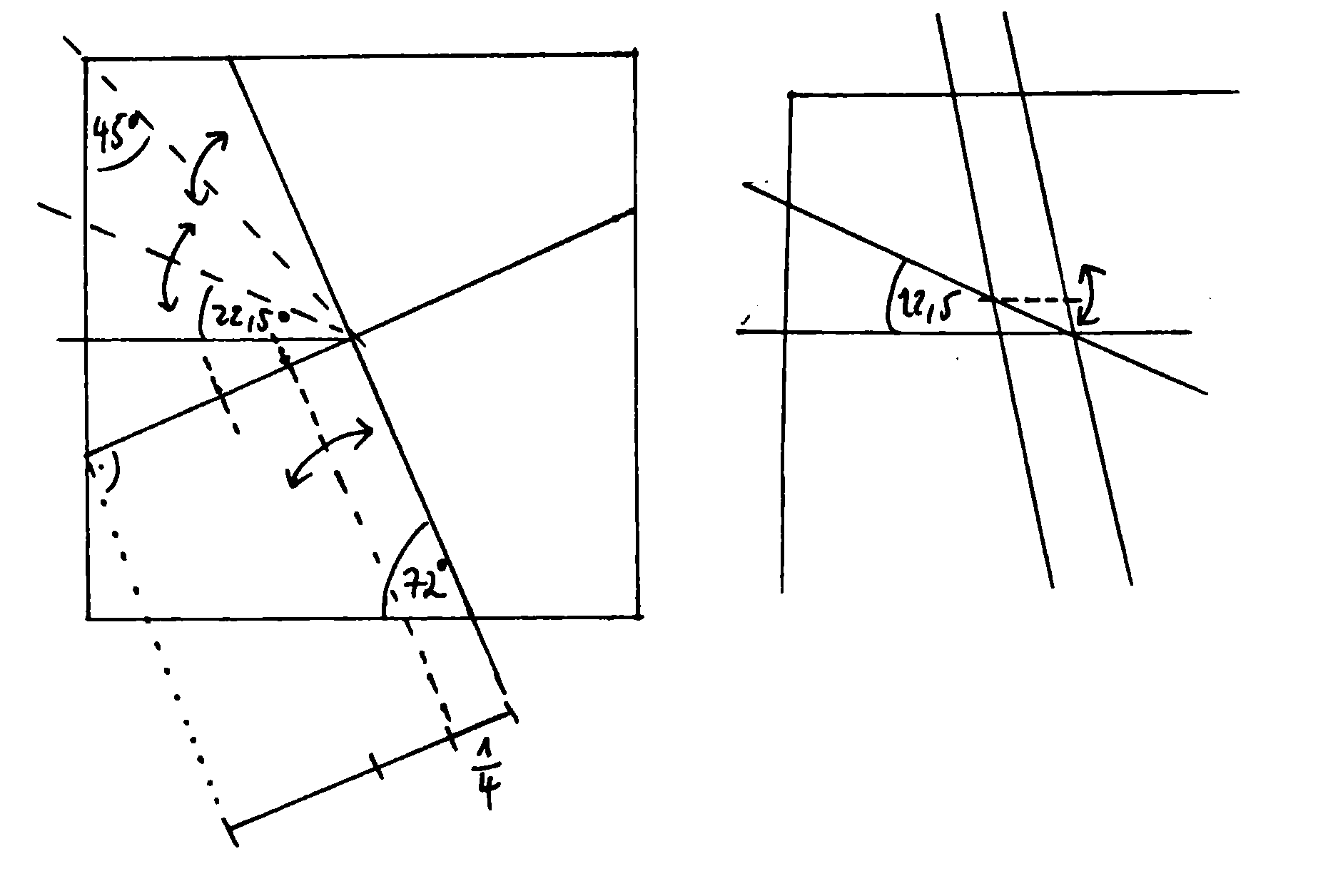
Mit dem letzten Schritt hat man die Seitenlänge eines Fünfecks bestimmt. Jetzt kann man die Fünfecke vervollständigen, indem man entlang der 72°-Mitteldiagonalen faltet und die Referenzlänge aus dem Letzten Schritt durchpaust, also durch die Schichten faltet. Für die übrigen Falten orientiert man sich am Crease Pattern, es sind keine weiteren Referenzen notwendig.

Das Finden der Referenzlinien ist sehr mühselig, allerdings ist es so tatsächlich möglich, das Dodekaeder aus einem quadratischen Papier zu falten. (Ich habe es einmal ausprobiert.) Einfacher ist es, das Crease Pattern auszudrucken und entlang der Kanten zu falten. Außerdem hat man dann auch keine Referenzlinien auf den Seitenflächen.

Ein anderer, beliebter Ansatz zum Falten von Polyedern ist es, das Modell aus mehreren Modulen zusammenzusetzen. Ein Beispiel ist dieses modulare Origami Design für ein Dodekaeder von Jun Maekawa: