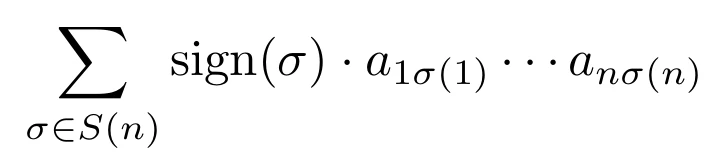How to write a matrix Permanent/Determinant function

We begin with the permanent.

Permanent formula: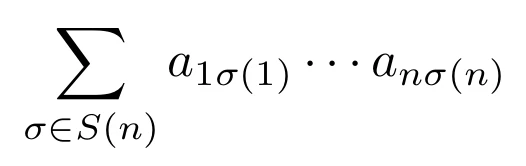

First, we need a way to compute the permutations of an array. Since we are not primarily aiming for efficiency, we can just use a simple recursive approach:
We want to reduce S(n) to S(n - 1). Let’s take an array [1, 2, 3, 4] that we want to generate permutations for. We can just choose a first element [1], calculate the permutations of [1, 2, 3, 4] without [1], i. e. [2, 3, 4], then add [1] as the first element to each of those. Then repeat with [2] and so on. The base case could be the empty array, in which we just return an empty array.

Modern Javascript allows us to express our code with an intuitive syntax: The algorithm loops through the input array, swaps the i-th element to the beginning, then calls itself recursively on the sub-array starting with the second element, finally swaps the first element back.

function S(arr) {
    const perm = [];
    for (let i = 0; i < arr.length; ++i) {
        [arr[0], arr[i]] = [arr[i], arr[0]];
        perm.push(...S(arr.slice(1)).map(s => [arr[0], ...s]));
        [arr[0], arr[i]] = [arr[i], arr[0]];
    }
    return arr.length ? perm : [[]];
}

By making more use of array functions, we can convert it into a more elegant one-liner:

const S = arr => arr.length ? arr.flatMap(first => S(arr
    .filter(e => e != first)).map(s => [first, ...s])) : [[]];

Now that we have the permutations, we have to multiply the matrix elements, then sum the result. We can do this with simple loops, or with Array.prototype.reduce:

const matrix = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
];
const permanent = S([0, 1, 2]).reduce((sum, s) => s.reduce(
    (prod, si, i) => prod * matrix[i][si], 1) + sum, 0);

Finally, we can get the determinant very easily using the Leibniz formula for determinants by adding a sign to each term depending on the permutation.

Leibniz formula for determinants: